[BOJ/JAVA] 백준 15988 / 1, 2, 3 더하기 3

• 시도횟수: 2회
• 시간: 약 20분
• 만족도: ★★★★☆
• 힌트 키워드: #dp

문제링크 : https://www.acmicpc.net/problem/1451

인트로

​ 실버라고 너무 만만하게 봐서 그랬는지, dp의 냄새는 났지만 바로 풀이법이 떠오르진 않았다. 1~4를 순서대로 써보니, (1,2,4,7) 이길래 여기서 눈치를 채고 풀었다.

문제 요약

• Input

  • 테스트 케이스의 개수 T
  • 정수 n

• output

  • n을 1, 2, 3의 합으로 나타내는 방법의 수를 출력

    예) n = 4

    • 1+1+1+1
    • 1+1+2
    • 1+2+1
    • 2+1+1
    • 2+2
    • 1+3
    • 3+1

접근 방식

1. DP

   

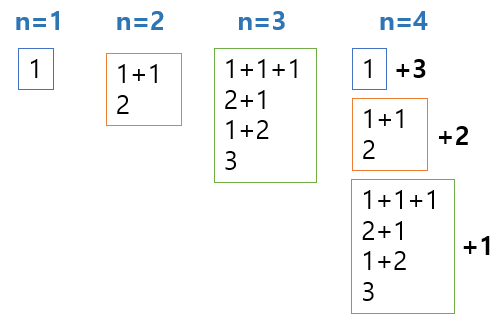
   dp[j]=dp[j-1]+dp[j-2]+dp[j-3] 의 점화식을 가진다.

오답 원인

오답: 1회

1. int 사용

   1000000009로 나누기 때문에 오버플로우가 안날 것이라고 판단을 하고 int를 사용했다. 바로 이전에 비슷한 이유로 틀려놓고 또 같은 실수를 해버리다닝,,, 아무튼 dp[j-1]+dp[j-2]+dp[j-3]을 하는 과정은 나누기 전이기 때문에 오버플로우가 발생할 수 있기 때문에, 오버플로우를 피하기 위해선 아래의 두 방법이 있는데 코드를 줄이기 위해 첫 번째 방법을 선택했다.

   • int배열을 long배열로 바꾸기
   • dp[j-1]%1000000009+dp[j-2]%1000000009+dp[j-3]%1000000009

정답 코드

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        Scanner sc = new Scanner(System.in);
        int range=1000001;
        long[] dp = new long[range];

        dp[1]=1;
        dp[2]=2;
        dp[3]=4;
        for (int j = 4; j < range; j++) {
            dp[j]=(dp[j-1]+dp[j-2]+dp[j-3])%1000000009;
        }

        int T = sc.nextInt();

        for (int i = 0; i < T; i++) {
            int N = sc.nextInt();
            System.out.println(dp[N]);
        }
    }
}

느낀점

1. 깔끔한 dp 문제

   접근법만 떠오른다면 너무나도 깔끔하게 코드가 작성돼서 재밌는 문제였다.

결과