[BOJ/JAVA] 백준 17071 / 숨바꼭질 5

문제링크 : https://www.acmicpc.net/problem/17071

인트로Permalink

문제를 처음 읽었을 때, 애매했던 부분이 있었다. 동생이 걷는 거도 왼쪽으로 갈 수 있는 건지 애매했었는데, 그러면 문제 난이도가 너무 높아지니까, 문제에 적혀있는 그대로만 보고 풀었다. 다행히 이게 맞았다.

원래의 BFS가 응용된 문제였는데, 재밌는 문제였다.

문제Permalink

• 요약Permalink

  • 수빈: 걷거나 순간이동
    • 걷기 - X → X-1 or X+1
    • 순간이동 - X → 2*X
  • 동생: 걷기
    • 걷기 - 매 초마다 이동, 가속 붙음 (이전에 이동한 거리보다 1을 더한 만큼 이동)
      • K, K+1, K+1+2, K+1+2+3
• 제한 사항
  • 수빈이가 0보다 작거나 50만보다 큰 좌표로 이동하는 것은 불가능
• Input
  • 수빈이가 있는 위치 N (0 ≤ N ≤ 500,000)
  • 동생이 있는 위치 K (0 ≤ K ≤ 500,000)
• output
  • 수빈이가 동생을 찾는 가장 빠른 시간 출력
  • 동생을 찾을 수 없거나, 찾는 위치가 500,000을 넘는 경우 -1 출력

접근 방식Permalink

1. 브루트포스 → 시간초과

   이 문제를 봤을 때, 시간을 고려하지 않는다면 바로 떠오르는 방법은 단순 탐색이다. Queue에 수빈이의 원래 위치 N을 넣어서 시작하고, poll된 값인 n에 대해 n+1, n-1, 2 *n 를 탐색하면 된다. t 초 후의 수빈이의 위치가 K+t *(t+1)/2 와 같다면 그 때의 t가 최소시간이다. 하지만, 이 방법은 약 3^t의 경우의 수를 탐색하기 때문에 당연히 시간초과가 발생한다. 시간을 줄이기 위해선 어떤 방법이 있을까?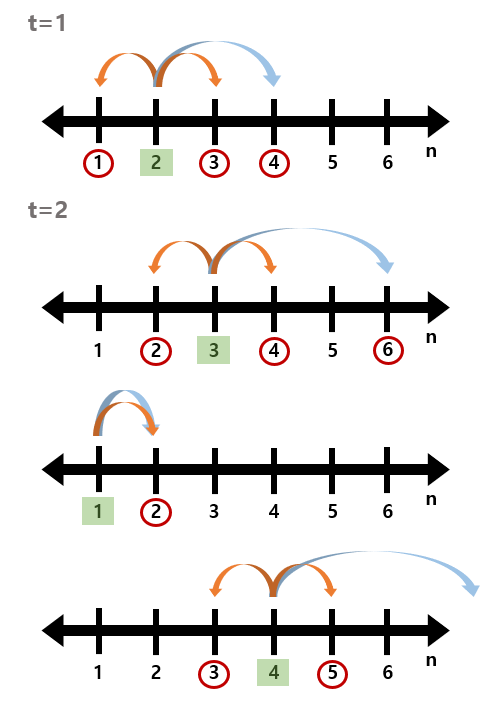

   

2. BFS

   위치에 범위는 0 ≤ N ≤ 500,000 이다. 왔던 곳을 기록한다면 시간을 크게 단축할 수 있을 것이다. 하지만 기존의 BFS 처럼 visited(boolean) 배열을 사용할 수 없다. t가 짝수일 때와 홀수일 때로 나눠서 생각해보면 단순해진다. 짝수인 시간에 n의 위치에 도착한다면, 그 이후의 걷기를 통해 이후에 짝수 시간엔 n의 위치에 돌아올 수 있다. 홀수일 때도 마찬가지이다. 따라서 기존의 visited 배열을 다음과 같이 설정하여 이 문제를 풀면 된다.

   • visited = int[500001][2]

   • visited[위치][홀짝] : 해당 위치에 최초로 도착한 홀/짝 시간

   그리고 이후, 동생을 찾을 수 있는지 유무를 판단하기 위해야 한다. Queue 밖에서 판단 로직을 짜도 되지만, 시간 절약을 위해 Queue 안에서 바로 체크했다. 현재 시간 t의 홀/짝 기준(t%2)으로 동생이 있을 위치 (K+t *(t+1)/2 ) 에 수빈이가 방문했으면, 반복문에서 빠져나와 해당 시간을 출력한다.

정답 코드Permalink

import java.util.*;

public class Main {
	static class Node{
		int n,t;
		Node(int n, int t){
			this.n=n;
			this.t=t;
		}
	}
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int N = sc.nextInt();
		int K = sc.nextInt();
		
		int ans=-1;
		
		int[][] visit = new int[500001][2];
		
		Queue<Node> q = new LinkedList<>();
		
		q.add(new Node(N,1));
		visit[N][1] = 1;
		
		while(!q.isEmpty()) {
			Node now = q.poll();
			int n=now.n;
			int isOdd = now.t%2;
			int t = visit[n][isOdd];
			
			int dis = K+(t-1)*(t)/2;
			if(dis>500000) break;
			if (visit[dis][isOdd]!=0) {
				ans=t-1;
				break;
			}
			
			int[] arr = {n+1,n-1,2*n};
			
			for (int i = 0; i < 3; i++) {
				int nN = arr[i];
				if(nN<0||nN>500000) continue;
				
				if(visit[nN][(isOdd+1)%2]==0) {
					visit[nN][(isOdd+1)%2]=t+1;
					q.add(new Node(nN,t+1));
					
				}
			}
		}
		sc.close();
		System.out.print(ans);
	}
}

결과Permalink